Wsrtjtyk

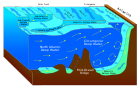
In fluid dynamics, the Craik–Leibovich (CL) vortex force describes a forcing of the mean flow through wave–current interaction, specifically between the Stokes drift velocity and the mean-flow vorticity. The CL vortex force is used to explain the generation of Langmuir circulations by an instability mechanism. The CL vortex-force mechanism was derived and studied by Sidney Leibovich and Alex D.D. Craik in the 1970s and 80s, in their studies of Langmuir circulations (discovered by Irving Langmuir in the 1930s).

Description

The CL vortex force is

ρuS×ω,{displaystyle rho ,{boldsymbol {u}}_{S}times {boldsymbol {omega }},}

with uS{displaystyle {boldsymbol {u}}_{S}} the (Lagrangian) Stokes drift velocity and vorticity ω=∇×u{displaystyle {boldsymbol {omega }}=nabla times {boldsymbol {u}}} (i.e. the curl of the Eulerian mean-flow velocity u{displaystyle {boldsymbol {u}}}). Further ρ{displaystyle rho } is the fluid density and ∇×{displaystyle nabla times } is the curl operator.

The CL vortex force finds its origins in the appearance of the Stokes drift in the convective acceleration terms in the mean momentum equation of the Euler equations or Navier–Stokes equations. For constant density, the momentum equation (divided by the density ρ{displaystyle rho }) is:^[1]

∂tu⏟(a)+u⋅∇u⏟(b)+2Ω×u⏟(c)+2Ω×uS⏟(d)+∇(π+u⋅uS)⏟(e)=uS×(∇×u)⏟(f)+ν∇⋅∇u⏟(g),{displaystyle underbrace {partial _{t}{boldsymbol {u}}} _{text{(a)}}+underbrace {{boldsymbol {u}}cdot nabla {boldsymbol {u}}} _{text{(b)}}+underbrace {2{boldsymbol {Omega }}times {boldsymbol {u}}} _{text{(c)}}+underbrace {2{boldsymbol {Omega }}times {boldsymbol {u}}_{S}} _{text{(d)}}+underbrace {nabla (pi +{boldsymbol {u}}cdot {boldsymbol {u}}_{S})} _{text{(e)}}=underbrace {{boldsymbol {u}}_{S}times (nabla times {boldsymbol {u}})} _{text{(f)}}+underbrace {nu ,nabla cdot nabla {boldsymbol {u}}} _{text{(g)}},}

with

• (a): temporal acceleration


• (b): convective acceleration


• (c): Coriolis force due to the angular velocity Ω{displaystyle {boldsymbol {Omega }}} of the Earth's rotation
  


• (d): Coriolis–Stokes force
  


• (e): gradient of the augmented pressure
  


• (f): Craik–Leibovich vortex force


• (g): viscous force due to the kinematic viscosity ν{displaystyle nu }
  

The CL vortex force can be obtained by several means. Originally, Craik and Leibovich used perturbation theory. An easy way to derive it is through the generalized Lagrangian mean theory.^[1] It can also be derived through a Hamiltonian mechanics description.^[2]

Notes

References