Wsrtjtyk

6-simplex
Type	uniform polypeton
Schläfli symbol	{35}
Coxeter diagrams
Elements	f5 = 7, f4 = 21, C = 35, F = 35, E = 21, V = 7 (χ=0)
Coxeter group	A6, [35], order 5040
Bowers name and (acronym)	Heptapeton (hop)
Vertex figure	5-simplex
Circumradius	0.645497
Properties	convex, isogonal self-dual

In geometry, a 6-simplex is a self-dual regular 6-polytope. It has 7 vertices, 21 edges, 35 triangle faces, 35 tetrahedral cells, 21 5-cell 4-faces, and 7 5-simplex 5-faces. Its dihedral angle is cos⁻¹(1/6), or approximately 80.41°.

Alternate names

It can also be called a heptapeton, or hepta-6-tope, as a 7-facetted polytope in 6-dimensions. The name heptapeton is derived from hepta for seven facets in Greek and -peta for having five-dimensional facets, and -on. Jonathan Bowers gives a heptapeton the acronym hop.^[1]

As a configuration

This configuration matrix represents the 6-simplex. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.^[2][3]

[76152015622151010533354644643533510105212615201567]{displaystyle {begin{bmatrix}{begin{matrix}7&6&15&20&15&6\2&21&5&10&10&5\3&3&35&4&6&4\4&6&4&35&3&3\5&10&10&5&21&2\6&15&20&15&6&7end{matrix}}end{bmatrix}}}

Coordinates

The Cartesian coordinates for an origin-centered regular heptapeton having edge length 2 are:

(1/21, 1/15, 1/10, 1/6, 1/3, ±1){displaystyle left({sqrt {1/21}}, {sqrt {1/15}}, {sqrt {1/10}}, {sqrt {1/6}}, {sqrt {1/3}}, pm 1right)}

(1/21, 1/15, 1/10, 1/6, −21/3, 0){displaystyle left({sqrt {1/21}}, {sqrt {1/15}}, {sqrt {1/10}}, {sqrt {1/6}}, -2{sqrt {1/3}}, 0right)}

(1/21, 1/15, 1/10, −3/2, 0, 0){displaystyle left({sqrt {1/21}}, {sqrt {1/15}}, {sqrt {1/10}}, -{sqrt {3/2}}, 0, 0right)}

(1/21, 1/15, −22/5, 0, 0, 0){displaystyle left({sqrt {1/21}}, {sqrt {1/15}}, -2{sqrt {2/5}}, 0, 0, 0right)}

(1/21, −5/3, 0, 0, 0, 0){displaystyle left({sqrt {1/21}}, -{sqrt {5/3}}, 0, 0, 0, 0right)}

(−12/7, 0, 0, 0, 0, 0){displaystyle left(-{sqrt {12/7}}, 0, 0, 0, 0, 0right)}

The vertices of the 6-simplex can be more simply positioned in 7-space as permutations of:

(0,0,0,0,0,0,1)

This construction is based on facets of the 7-orthoplex.

Images

orthographic projections

AkCoxeter plane	A6	A5	A4
Graph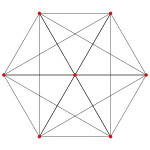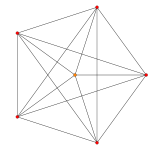
Dihedral symmetry	[7]	[6]	[5]
Ak Coxeter plane	A3	A2
Graph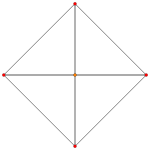
Dihedral symmetry	[4]	[3]

Related uniform 6-polytopes

The regular 6-simplex is one of 35 uniform 6-polytopes based on the [3,3,3,3,3] Coxeter group, all shown here in A₆Coxeter plane orthographic projections.

A6 polytopes
t0	t1	t2	t0,1	t0,2	t1,2	t0,3	t1,3	t2,3
t0,4	t1,4	t0,5	t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4	t0,2,4
t1,2,4	t0,3,4	t0,1,5	t0,2,5	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,2,3,4	t1,2,3,4
t0,1,2,5	t0,1,3,5	t0,2,3,5	t0,1,4,5	t0,1,2,3,4	t0,1,2,3,5	t0,1,2,4,5	t0,1,2,3,4,5

Notes

References

• 
  H.S.M. Coxeter:
  
  
  
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
    ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  
  
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  
  
  • 
    Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
    ISBN 978-0-471-01003-6 [1]
    
    
    
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    
    
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    
    
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
    
    
    
    
  
  
  
  


• 
  John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008,
  ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)


• 
  Norman Johnson Uniform Polytopes, Manuscript (1991)
  
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
  
  


• 
  Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o3o3o - hix".
  

External links

• 
  Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
  


• Polytopes of Various Dimensions


• Multi-dimensional Glossary