Wsrtjtyk

Cubic honeycomb
Type	Regular honeycomb
Family	Hypercube honeycomb
Indexing[1]	J11,15, A1 W1, G22
Schläfli symbol	{4,3,4}
Coxeter diagram
Cell type	{4,3}
Face type	{4}
Vertex figure	(octahedron)
Space group Fibrifold notation	Pm3m (221) 4−:2
Coxeter group	C~3{displaystyle {tilde {C}}_{3}}, [4,3,4]
Dual	self-dual Cell:
Properties	vertex-transitive, regular

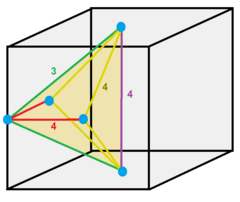
The cubic honeycomb or cubic cellulation is the only regular space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Cartesian coordinates

Simple cubic

The Cartesian coordinates of the vertices are:

(i, j, k)

for all integral values: i,j,k, with edges parallel to the axes and with an edge length of 1.

Related honeycombs

It is part of a multidimensional family of hypercube honeycombs, with Schläfli symbols of the form {4,3,...,3,4}, starting with the square tiling, {4,4} in the plane.

It is one of 28 uniform honeycombs using convex uniform polyhedral cells.

Isometries of simple cubic lattices

Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems:

Crystal system	Monoclinic Triclinic	Orthorhombic	Tetragonal	Rhombohedral	Cubic
Unit cell	Parallelepiped	Rectangular cuboid	Square cuboid	Trigonal trapezohedron	Cube
Point group Order Rotation subgroup	[ ], (*) Order 2 [ ]+, (1)	[2,2], (*222) Order 8 [2,2]+, (222)	[4,2], (*422) Order 16 [4,2]+, (422)	[3], (*33) Order 6 [3]+, (33)	[4,3], (*432) Order 48 [4,3]+, (432)
Diagram
Space group Rotation subgroup	Pm (6) P1 (1)	Pmmm (47) P222 (16)	P4/mmm (123) P422 (89)	R3m (160) R3 (146)	Pm3m (221) P432 (207)
Coxeter notation	-	[∞]a×[∞]b×[∞]c	[4,4]a×[∞]c	-	[4,3,4]a
Coxeter diagram	-			-

Uniform colorings

There is a large number of uniform colorings, derived from different symmetries. These include:

Coxeter notation Space group	Coxeter diagram	Schläfli symbol	Partial honeycomb	Colors by letters
[4,3,4] Pm3m (221)	=	{4,3,4}		1: aaaa/aaaa
[4,31,1] = [4,3,4,1+] Fm3m (225)	=	{4,31,1}		2: abba/baab
[4,3,4] Pm3m (221)		t0,3{4,3,4}		4: abbc/bccd
[[4,3,4]] Pm3m (229)		t0,3{4,3,4}		4: abbb/bbba
[4,3,4,2,∞]	or	{4,4}×t{∞}		2: aaaa/bbbb
[4,3,4,2,∞]		t1{4,4}×{∞}		2: abba/abba
[∞,2,∞,2,∞]		t{∞}×t{∞}×{∞}		4: abcd/abcd
[∞,2,∞,2,∞] = [4,(3,4)*]	=	t{∞}×t{∞}×t{∞}		8: abcd/efgh

Projections

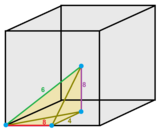
The cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a triangular tiling. A square symmetry projection forms a square tiling.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame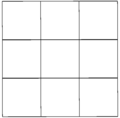

Related polytopes and honeycombs

It is related to the regular 4-polytope tesseract, Schläfli symbol {4,3,3}, which exists in 4-space, and only has 3 cubes around each edge. It's also related to the order-5 cubic honeycomb, Schläfli symbol {4,3,5}, of hyperbolic space with 5 cubes around each edge.

It is in a sequence of polychora and honeycomb with octahedral vertex figures.

{p,3,4} regular honeycombs
Space	S3	E3	H3
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

It in a sequence of regular polytopes and honeycombs with cubic cells.

{4,3,p} regular honeycombs
Space	S3	E3	H3
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{p,3,p} regular honeycombs
Space	S3	Euclidean E3	H3
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Related Euclidean tessellations

The [4,3,4], , Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.

C3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4−:2	[4,3,4]		×1	1, 2, 3, 4, 5, 6
Fm3m (225)	2−:2	[1+,4,3,4] ↔ [4,31,1]	↔	Half	7, 11, 12, 13
I43m (217)	4o:2	[[(4,3,4,2+)]]		Half × 2	(7),
Fd3m (227)	2+:2	[[1+,4,3,4,1+]] ↔ [[3[4]]]	↔	Quarter × 2	10,
Im3m (229)	8o:2	[[4,3,4]]		×2	(1), 8, 9

The [4,3^1,1], , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.

B3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2−:2	[4,31,1] ↔ [4,3,4,1+]	↔	×1	1, 2, 3, 4
Fm3m (225)	2−:2	<[1+,4,31,1]> ↔ <[3[4]]>	↔	×2	(1), (3)
Pm3m (221)	4−:2	<[4,31,1]>		×2	5, 6, 7, (6), 9, 10, 11

This honeycomb is one of five distinct uniform honeycombs^[2] constructed by the A~3{displaystyle {tilde {A}}_{3}} Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:

A3 honeycombs
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1o:2	a1	[3[4]]		A~3{displaystyle {tilde {A}}_{3}}	(None)
Fm3m (225)	2−:2	d2	<[3[4]]> ↔ [4,31,1]	↔	A~3{displaystyle {tilde {A}}_{3}}×21 ↔ B~3{displaystyle {tilde {B}}_{3}}	1, 2
Fd3m (227)	2+:2	g2	[[3[4]]] or [2+[3[4]]]	↔	A~3{displaystyle {tilde {A}}_{3}}×22	3
Pm3m (221)	4−:2	d4	<2[3[4]]> ↔ [4,3,4]	↔	A~3{displaystyle {tilde {A}}_{3}}×41 ↔ C~3{displaystyle {tilde {C}}_{3}}	4
I3 (204)	8−o	r8	[4[3[4]]]+ ↔ [[4,3+,4]]	↔	½A~3{displaystyle {tilde {A}}_{3}}×8 ↔ ½C~3{displaystyle {tilde {C}}_{3}}×2	(*)
Im3m (229)	8o:2		[4[3[4]]] ↔ [[4,3,4]]		A~3{displaystyle {tilde {A}}_{3}}×8 ↔ C~3{displaystyle {tilde {C}}_{3}}×2	5

Rectified cubic honeycomb

Rectified cubic honeycomb
Type	Uniform honeycomb
Cells	Octahedron Cuboctahedron
Schläfli symbol	r{4,3,4} or t1{4,3,4} r{4,31,1} 2r{4,31,1} r{3[4]}
Coxeter diagrams	= = = = =
Vertex figure	Cuboid
Space group Fibrifold notation	Pm3m (221) 4−:2
Coxeter group	C~3{displaystyle {tilde {C}}_{3}}, [4,3,4]
Dual	oblate octahedrille Cell:
Properties	vertex-transitive, edge-transitive

The rectified cubic honeycomb or rectified cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.

John Horton Conway calls this honeycomb a cuboctahedrille, and its dual an oblate octahedrille.

Projections

The rectified cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame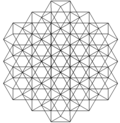

Symmetry

There are four uniform colorings for the cells of this honeycomb with reflective symmetry, listed by their Coxeter group, and Wythoff construction name, and the Coxeter diagram below.

Symmetry	[4,3,4] C~3{displaystyle {tilde {C}}_{3}}	[1+,4,3,4] [4,31,1], B~3{displaystyle {tilde {B}}_{3}}	[4,3,4,1+] [4,31,1], B~3{displaystyle {tilde {B}}_{3}}	[1+,4,3,4,1+] [3[4]], A~3{displaystyle {tilde {A}}_{3}}
Space group	Pm3m (221)	Fm3m (225)	Fm3m (225)	F43m (216)
Coloring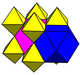
Coxeter diagram
Vertex figure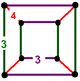
Vertex figure symmetry	D4h [4,2] (*224) order 16	D2h [2,2] (*222) order 8	C4v [4] (*44) order 8	C2v [2] (*22) order 4

This honeycomb can be divided on trihexagonal tiling planes, using the hexagon centers of the cuboctahedra, creating two triangular cupolae. This scaliform honeycomb is represented by Coxeter diagram , and symbol s₃{2,6,3}, with coxeter notation symmetry [2⁺,6,3].

.

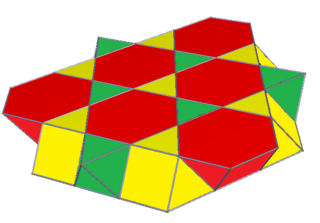Truncated cubic honeycomb

Truncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t{4,3,4} or t0,1{4,3,4} t{4,31,1}
Coxeter diagrams	=
Cell type	3.8.8, {3,4}
Face type	{3}, {4}, {8}
Vertex figure	Isosceles square pyramid
Space group Fibrifold notation	Pm3m (221) 4−:2
Coxeter group	C~3{displaystyle {tilde {C}}_{3}}, [4,3,4]
Dual	Pyramidille Cell:
Properties	vertex-transitive

The truncated cubic honeycomb or truncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1.

John Horton Conway calls this honeycomb a truncated cubille, and its dual pyramidille.

Projections

The truncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Symmetry

There is a second uniform coloring by reflectional symmetry of the Coxeter groups, the second seen with alternately colored truncated cubic cells.

Construction	Bicantellated alternate cubic	Truncated cubic honeycomb
Coxeter group	[4,31,1], B~3{displaystyle {tilde {B}}_{3}}	[4,3,4], C~3{displaystyle {tilde {C}}_{3}} =<[4,31,1]>
Space group	Fm3m	Pm3m
Coloring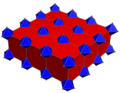
Coxeter diagram	=
Vertex figure

Alternated bitruncated cubic honeycomb

Alternated bitruncated cubic honeycomb
Type	Nonuniform honeycomb
Schläfli symbol	2s{4,3,4} 2s{4,31,1} sr{3[4]}
Coxeter diagrams	= = =
Cells	tetrahedron icosahedron
Vertex figure
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Properties	vertex-transitive

The alternated bitruncated cubic honeycomb or bisnub cubic honeycomb can be creating regular icosahedron from the truncated octahedra with irregular tetrahedral cells created in the gaps. There are three constructions from three related Coxeter diagrams: , , and . These have symmetry [4,3⁺,4], [4,(3^1,1)⁺] and [3^[4]]⁺ respectively. The first and last symmetry can be doubled as [[4,3⁺,4]] and [[3^[4]]]⁺.

This honeycomb is represented in the boron atoms of the α-rhombihedral crystal. The centers of the icosahedra are located at the fcc positions of the lattice.^[3]

Five uniform colorings

Space group	I3 (204)	Pm3 (200)	Fm3 (202)	Fd3 (203)	F23 (196)
Fibrifold	8−o	4−	2−	2o+	1o
Coxeter group	[[4,3+,4]]	[4,3+,4]	[4,(31,1)+]	[[3[4]]]+	[3[4]]+
Coxeter diagram
Order	double	full	half	quarter double	quarter

Cantellated cubic honeycomb

Cantellated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	rr{4,3,4} or t0,2{4,3,4} rr{4,31,1}
Coxeter diagram	=
Cells	rr{4,3} r{4,3} {4,3}
Vertex figure	(Wedge)
Space group Fibrifold notation	Pm3m (221) 4−:2
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Dual	quarter oblate octahedrille Cell:
Properties	vertex-transitive

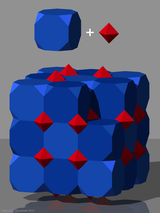
The cantellated cubic honeycomb or cantellated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedra, cuboctahedra, and cubes in a ratio of 1:1:3.

John Horton Conway calls this honeycomb a 2-RCO-trille, and its dual quarter oblate octahedrille.

Images

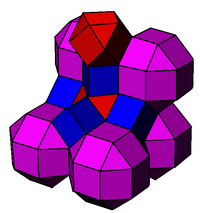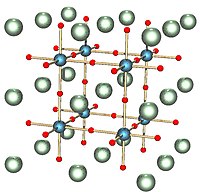It is closely related to the perovskite structure, shown here with cubic symmetry, with atoms placed at the center of the cells of this honeycomb.

Projections

The cantellated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame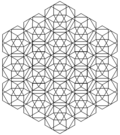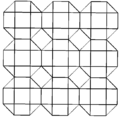

Symmetry

There is a second uniform colorings by reflectional symmetry of the Coxeter groups, the second seen with alternately colored rhombicuboctahedral cells.

Vertex uniform colorings by cell

Construction	Truncated cubic honeycomb	Bicantellated alternate cubic
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}} =<[4,31,1]>	[4,31,1], B~3{displaystyle {tilde {B}}_{3}}
Space group	Pm3m	Fm3m
Coxeter diagram
Coloring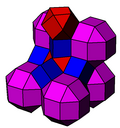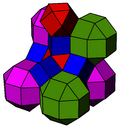
Vertex figure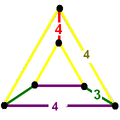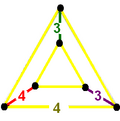
Vertex figure symmetry	[ ] order 2	[ ]+ order 1

Quarter oblate octahedrille

The dual of the cantellated cubic honeycomb is called a quarter oblate octahedrille, a catoptric tessellation with Coxeter diagram , containing faces from two of four hyperplanes of the cubic [4,3,4] fundamental domain.

It has irregular triangle bipyramid cells which can be seen as 1/12 of a cube, made from the cube center, 2 face centers, and 2 vertices.

Cantitruncated cubic honeycomb

Cantitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	tr{4,3,4} or t0,1,2{4,3,4} tr{4,31,1}
Coxeter diagram	=
Vertex figure	(Irreg. tetrahedron)
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Space group Fibrifold notation	Pm3m (221) 4−:2
Dual	triangular pyramidille Cells:
Properties	vertex-transitive

The cantitruncated cubic honeycomb or cantitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of truncated cuboctahedra, truncated octahedra, and cubes in a ratio of 1:1:3.

John Horton Conway calls this honeycomb a n-tCO-trille, and its dual triangular pyramidille.

Images

Four cells exist around each vertex:

Projections

The cantitruncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid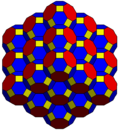
Frame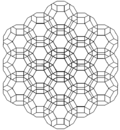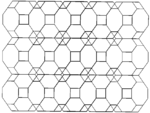

Symmetry

Cells can be shown in two different symmetries. The linear Coxeter diagram form can be drawn with one color for each cell type. The bifurcating diagram form can be drawn with two types (colors) of truncated cuboctahedron cells alternating.

Construction	Cantitruncated cubic	Omnitruncated alternate cubic
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}} =<[4,31,1]>	[4,31,1], B~3{displaystyle {tilde {B}}_{3}}
Space group	Pm3m (221)	Fm3m (225)
Fibrifold	4−:2	2−:2
Coloring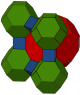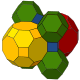
Coxeter diagram
Vertex figure
Vertex figure symmetry	[ ] order 2	[ ]+ order 1

Triangular pyramidille

The dual of the cantitruncated cubic honeycomb is called a triangular pyramidille, with Coxeter diagram, . This honeycomb cells represents the fundamental domains of B~3{displaystyle {tilde {B}}_{3}} symmetry.

A cell can be as 1/24 of a translational cube with vertices positioned: taking two corner, ne face center, and the cube center. The edge colors and labels specify how many cells exist around the edge.

Related polyhedra and honeycombs

It is related to a skew apeirohedron with vertex configuration 4.4.6.6, with the octagons and some of the squares removed. It can be seen as constructed by augmenting truncated cuboctahedral cells, or by augmenting alternated truncated octahedra and cubes.

Two views

Alternated cantitruncated cubic honeycomb

Alternated cantitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	sr{4,3,4} sr{4,31,1}
Coxeter diagrams	=
Cells	tetrahedron pseudoicosahedron snub cube
Vertex figure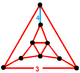
Coxeter group	[4,31,1], B~3{displaystyle {tilde {B}}_{3}}
Dual	Cell: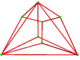
Properties	vertex-transitive

The alternated cantitruncated cubic honeycomb or snub rectified cubic honeycomb contains three types of cells: snub cubes, icosahedra (snub tetrahedron), and tetrahedra. In addition the gaps created at the alternated vertices form tetrahedral cells.
Although it is not uniform, constructionally it can be given as Coxeter diagrams or .

Runcic cantitruncated cubic honeycomb

Runcic cantitruncated cubic honeycomb
Type	Convex honeycomb
Schläfli symbol	sr3{4,3,4}
Coxeter diagrams
Cells	rhombicuboctahedron snub cube cube
Vertex figure
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Dual
Properties	vertex-transitive

The runcic cantitruncated cubic honeycomb or runcic cantitruncated cubic cellulation contains cells: snub cubes, rhombicuboctahedrons, and cubes. In addition the gaps created at the alternated vertices form an irregular cell.
Although it is not uniform, constructionally it can be given as Coxeter diagram .

Runcitruncated cubic honeycomb

Runcitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t0,1,3{4,3,4}
Coxeter diagrams
Cells	rhombicuboctahedron truncated cube octagonal prism cube
Vertex figure	(Trapezoidal pyramid)
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Space group Fibrifold notation	Pm3m (221) 4−:2
Dual	square quarter pyramidille Cell
Properties	vertex-transitive

The runcitruncated cubic honeycomb or runcitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedra, truncated cubes, octagonal prisms, and cubes in a ratio of 1:1:3:3.

Its name is derived from its Coxeter diagram, with three ringed nodes representing 3 active mirrors in the Wythoff construction from its relation to the regular cubic honeycomb.

John Horton Conway calls this honeycomb a 1-RCO-trille, and its dual square quarter pyramidille.

Projections

The runcitruncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame

Related skew apeirohedron

A related uniform skew apeirohedron exists with the same vertex arrangement, but some of the square and all of the octagons removed. It can be seen as truncated tetrahedra and truncated cubes augmented together.

Square quarter pyramidille

The dual to the runcitruncated cubic honeycomb is called a square quarter pyramidille, with Coxeter diagram . Faces exist in 3 of 4 hyperplanes of the [4,3,4], C~3{displaystyle {tilde {C}}_{3}} Coxeter group.

Cells are irregular pyramids and can be seen as 1/24 of a cube, using one corner, one mid-edge point, two face centers, and the cube center.

Omnitruncated cubic honeycomb

Omnitruncated cubic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t0,1,2,3{4,3,4}
Coxeter diagram
Vertex figure	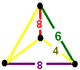Phyllic disphenoid
Space group Fibrifold notation Coxeter notation	Im3m (229) 8o:2 [[4,3,4]]
Coxeter group	[4,3,4], C~3{displaystyle {tilde {C}}_{3}}
Dual	eighth pyramidille Cell
Properties	vertex-transitive

The omnitruncated cubic honeycomb or omnitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cuboctahedra and octagonal prisms in a ratio of 1:3.

John Horton Conway calls this honeycomb a b-tCO-trille, and its dual eighth pyramidille.

Projections

The omnitruncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements.

Orthogonal projections

Symmetry	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
Frame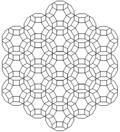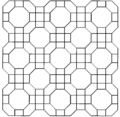

Symmetry

Cells can be shown in two different symmetries. The Coxeter diagram form has two colors of truncated cuboctahedra and octagonal prisms. The symmetry can be doubled by relating the first and last branches of the Coxeter diagram, which can be shown with one color for all the truncated cuboctahedral and octagonal prism cells.

Two uniform colorings

Symmetry	C~3{displaystyle {tilde {C}}_{3}}, [4,3,4]	C~3{displaystyle {tilde {C}}_{3}}×2, [[4,3,4]]
Space group	Pm3m (221)	Im3m (229)
Fibrifold	4−:2	8o:2
Coloring
Coxeter diagram
Vertex figure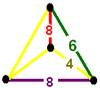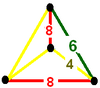

Related polyhedra

Two related uniform skew apeirohedron exist with the same vertex arrangement. The first has octagons removed, and vertex configuration 4.4.4.6. It can be seen as truncated cuboctahedra and octagonal prisms augmented together. The second can be seen as augmented octagonal prisms.

4.4.4.6	4.8.4.8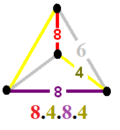

Alternated omnitruncated cubic honeycomb

Alternated omnitruncated cubic honeycomb
Type	Alternated uniform honeycomb
Schläfli symbol	ht0,1,2,3{4,3,4}
Coxeter diagram
Cells	snub cube square antiprism tetrahedron
Vertex figure
Symmetry	[[4,3,4]]+
Dual	Phyllic disphenoidal honeycomb
Properties	vertex-transitive

A alternated omnitruncated cubic honeycomb orfull snub cubic honeycomb can be constructed by alternation of the omnitruncated cubic honeycomb, although it can not be made uniform, but it can be given Coxeter diagram: and has symmetry [[4,3,4]]⁺. It makes snub cubes from the truncated cuboctahedra, square antiprisms from the octagonal prisms and with new tetrahedral cells created in the gaps.

Dual alternated omnitruncated cubic honeycomb

Dual alternated omnitruncated cubic honeycomb
Type	Dual alternated uniform honeycomb
Schläfli symbol	dht0,1,2,3{4,3,4}
Coxeter diagram
Cells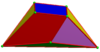
Symmetry	[[4,3,4]]+
Properties	Cell-transitive

A dual alternated omnitruncated cubic honeycomb is a space-filling honeycomb constructed as the dual of the alternated omnitruncated cubic honeycomb.

Cells can be seen from tetrahedra as 1/48 of a cube, augmented by new center point of adjacent tetrahedra.

24 cells fit around a vertex, making a chiral octahedral symmetry that can be stacked in all 3-dimensions:

Individual cells have 2-fold rotational symmetry. In 2D orthogonal projection, this looks like a mirror symmetry.

Cell views

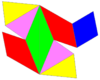Net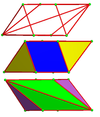

Truncated square prismatic honeycomb

Truncated square prismatic honeycomb
Type	Uniform honeycomb
Schläfli symbol	t{4,4}×{∞} or t0,1,3{4,4,2,∞} tr{4,4}×{∞} or t0,1,2,3{4,4,∞}
Coxeter-Dynkin diagram
Coxeter group	[4,4,2,∞]
Dual	Tetrakis square prismatic tiling Cell:
Properties	vertex-transitive

The truncated square prismatic honeycomb or tomo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octagonal prisms and cubes in a ratio of 1:1.

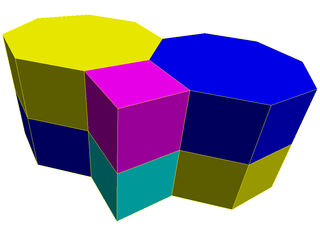
It is constructed from a truncated square tiling extruded into prisms.

It is one of 28 convex uniform honeycombs.

Snub square prismatic honeycomb

Snub square prismatic honeycomb
Type	Uniform honeycomb
Schläfli symbol	s{4,4}×{∞} sr{4,4}×{∞}
Coxeter-Dynkin diagram
Coxeter group	[4+,4,2,∞] [(4,4)+,2,∞]
Dual	Cairo pentagonal prismatic honeycomb Cell:
Properties	vertex-transitive

The snub square prismatic honeycomb or simo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.

It is constructed from a snub square tiling extruded into prisms.

It is one of 28 convex uniform honeycombs.

See also

Wikimedia Commons has media related to Cubic honeycomb.

• Architectonic and catoptric tessellation


• Alternated cubic honeycomb


• List of regular polytopes


• 
  Order-5 cubic honeycomb A hyperbolic cubic honeycomb with 5 cubes per edge


• voxel

References

• 
  John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
  ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)


• 
  Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition,
  ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs


• George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
  


• 
  Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.


• 
  Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
  ISBN 978-0-471-01003-6 [2]
  
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
  
  


• 
  A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.


• 
  Klitzing, Richard. "3D Euclidean Honeycombs x4o3o4o - chon - O1".
  


• Uniform Honeycombs in 3-Space: 01-Chon

v t e Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	A~n−1{displaystyle {tilde {A}}_{n-1}}	C~n−1{displaystyle {tilde {C}}_{n-1}}	B~n−1{displaystyle {tilde {B}}_{n-1}}	D~n−1{displaystyle {tilde {D}}_{n-1}}	G~2{displaystyle {tilde {G}}_{2}} / F~4{displaystyle {tilde {F}}_{4}} / E~n−1{displaystyle {tilde {E}}_{n-1}}
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21