Wsrtjtyk

Counting using tally marks at Hanakapiai Beach. The number shown is 82.

Brahmi numerals (lower row) in India in the 1st century CE. Note the similarity of the first three numerals to the Chinese characters for one through three (一 二 三), plus the resemblance of both sets of numerals to horizontal tally marks.

Tally marks, also called hash marks, are a unary numeral system. They are a form of numeral used for counting. They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no intermediate results need to be erased or discarded.

However, because of the length of large numbers, tallies are not commonly used for static text. Notched sticks, known as tally sticks, were also historically used for this purpose.

Early history

Counting aids other than body parts appear in the Upper Paleolithic. The oldest tally sticks date to between 35,000 and 25,000 years ago, in the form of notched bones found in the context of the European Aurignacian to Gravettian and in Africa's Late Stone Age.

The so-called Wolf bone is a prehistoric artifact discovered in 1937 in Czechoslovakia during excavations at Vestonice, Moravia, led by Karl Absolon. Dated to the Aurignacian, approximately 30,000 years ago, the bone is marked with 55 marks which may be tally marks. The head of an ivory Venus figurine was excavated close to the bone.^[1]

The Ishango bone, found in the Ishango region of the present-day Democratic Republic of Congo, is dated to over 20,000 years old. Upon discovery, it was thought to portray a series of prime numbers. In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10."^[2]Alexander Marshack examined the Ishango bone microscopically, and concluded that it may represent a six-month lunar calendar.^[3]

Clustering

Various ways to cluster the number 8. The first or fifth mark in each group may be written at an angle to the others for easier distinction. In the fourth example, the fifth stroke "closes out" a group of five, forming a "herringbone". In the fifth row the fifth mark crosses diagonally, forming a "five-bar gate".

Tally marks are typically clustered in groups of five for legibility. The cluster size 5 has the advantages of (a) easy conversion into decimal for higher arithmetic operations and (b) avoiding error, as humans can far more easily correctly identify a cluster of 5 than one of 10.

• 
  

  

  
  

  
  

  Tally marks used in most of Europe, Zimbabwe, Australia, New Zealand and North America.
  In some variants, the diagonal/horizontal slash is used on its own when five or more units are added at once.
  

  
  

  
  


• 
  

  

  
  

  
  

  Cultures using Chinese characters tally by forming the character 正, which consists of five strokes.^[4][5]

  
  

  
  


• 
  

  

  
  

  
  

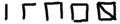
  Tally marks used in France, Spain, their former colonies and Brazil. 1 to 5 and so on. These are most commonly used for registering scores in card games, like Truco
  

  
  

  
  


• 
  

  

  
  

  
  

  In the dot and line (or dot-dash) tally, dots represent counts from 1 to 4, lines 5 to 8, and diagonal lines 9 and 10. This method is commonly used in forestry and related fields.^[6]

  
  

  
  


• 
  

  

  
  

  
  

  Brahmi numerals (lower row) in India in the 1st century CE
  

  
  

  
  

Writing systems

Roman numerals, the Chinese numerals for one through three (一 二 三), and rod numerals were derived from tally marks, as possibly was the ogham script.^[7]

Base 1 arithmetic notation system is an unary positional system similar to tally marks. It is rarely used as a practical base for counting due to its difficult readability. It is made by the concatenation of zero.

The numbers 1, 2, 3, 4, 5, ... would be represented in this system as^[8]

0, 00, 000, 0000, 00000, ...

Base 1 notation is widely used in type numbers of flour, the higher number represents a higher grind.

See also

Wikimedia Commons has media related to Unary numeral.

References