Wsrtjtyk

In combinatorial mathematics, Catalan's triangle is a number triangle whose entries C(n,k){displaystyle C(n,k)} give the number of strings consisting of n X's and k Y's such that no initial segment of the string has more Y's than X's. It is a generalization of the Catalan numbers, and is named after Eugène Charles Catalan. Bailey^[1] shows that C(n,k){displaystyle C(n,k)} satisfy the following properties:

1. 
   C(n,0)=1 for n≥0{displaystyle C(n,0)=1{text{ for }}ngeq 0}.


2. 
   C(n,1)=n for n≥1{displaystyle C(n,1)=n{text{ for }}ngeq 1}.


3. C(n+1,k)=C(n+1,k−1)+C(n,k) for 1<k<n+1{displaystyle C(n+1,k)=C(n+1,k-1)+C(n,k){text{ for }}1<k<n+1}


4. 
   C(n+1,n+1)=C(n+1,n) for n≥1{displaystyle C(n+1,n+1)=C(n+1,n){text{ for }}ngeq 1}.

Formula 3 shows that the entry in the triangle is obtained recursively by adding numbers to the left and above in the triangle. The earliest appearance of the Catalan triangle along with the recursion formula is in page 214 of the treatise on Calculus published in 1800^[2] by Louis François Antoine Arbogast.

Shapiro^[3] introduces another triangle which he calls the Catalan triangle that is distinct from the triangle being discussed here.

General formula

The general formula for C(n,k){displaystyle C(n,k)} is given by^[1][4]

C(n,k)=(n+k)!(n−k+1)k!(n+1)!,{displaystyle C(n,k)={frac {(n+k)!(n-k+1)}{k!(n+1)!}},}

where n and k are nonnegative integers and n! denotes the factorial. Thus, for k>0, C(n,k)=(n+kk)−(n+kk−1){displaystyle C(n,k)=left({begin{array}{c}n+k\kend{array}}right)-left({begin{array}{c}n+k\k-1end{array}}right)}.

The diagonal C(n, n) is the n-th Catalan number. The row sum of the n-th row is the (n + 1)-th Catalan number.

Some values are given by^[5]

n  k	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	2
3	1	3	5	5
4	1	4	9	14	14
5	1	5	14	28	42	42
6	1	6	20	48	90	132	132
7	1	7	27	75	165	297	429	429
8	1	8	35	110	275	572	1001	1430	1430

Generalization

Catalan's trapezoids are a countable set of number trapezoids which generalize Catalan’s triangle. Catalan's trapezoid of order m = 1, 2, 3, ... is a number trapezoid whose entries Cm(n,k){displaystyle C_{m}(n,k)} give the number of strings consisting of n X-s and k Y-s such that in every initial segment of the string the number of Y-s does not exceed the number of X-s by m or more.^[6] By definition, Catalan's trapezoid of order m = 1 is Catalan's triangle, i.e., C1(n,k)=C(n,k){displaystyle C_{1}(n,k)=C(n,k)}.

Some values of Catalan's trapezoid of order m = 2 are given by

n  k	0	1	2	3	4	5	6	7	8
0	1	1
1	1	2	2
2	1	3	5	5
3	1	4	9	14	14
4	1	5	14	28	42	42
5	1	6	20	48	90	132	132
6	1	7	27	75	165	297	429	429
7	1	8	35	110	275	572	1001	1430	1430

Some values of Catalan's trapezoid of order m = 3 are given by

n  k	0	1	2	3	4	5	6	7	8	9
0	1	1	1
1	1	2	3	3
2	1	3	6	9	9
3	1	4	10	19	28	28
4	1	5	15	34	62	90	90
5	1	6	21	55	117	207	297	297
6	1	7	28	83	200	407	704	1001	1001
7	1	8	36	119	319	726	1430	2431	3432	3432

Again, each element is the sum of the one above and the one to the left.

A general formula for Cm(n,k){displaystyle C_{m}(n,k)} is given by

Cm(n,k)={(n+kk)0≤k<m(n+kk)−(n+kk−m)m≤k≤n+m−10k>n+m−1{displaystyle C_{m}(n,k)={begin{cases}left({begin{array}{c}n+k\kend{array}}right)&,,,0leq k<m\\left({begin{array}{c}n+k\kend{array}}right)-left({begin{array}{c}n+k\k-mend{array}}right)&,,,mleq kleq n+m-1\\0&,,,k>n+m-1end{cases}}}

( n = 0, 1, 2, ..., k = 0, 1, 2, ..., m = 1, 2, 3, ...).

A proof of the general formula for Cm(n,k){displaystyle C_{m}(n,k)}

One proof of the general formula involves extension of the Andres Reflection method as used in the second proof for the Catalan number. The following shows how every path from the bottom left (0,0) to the top right (k, n) of the diagram that crosses the constraint n - k + m - 1 = 0 can also be reflected to the end point (n + m, k - m).

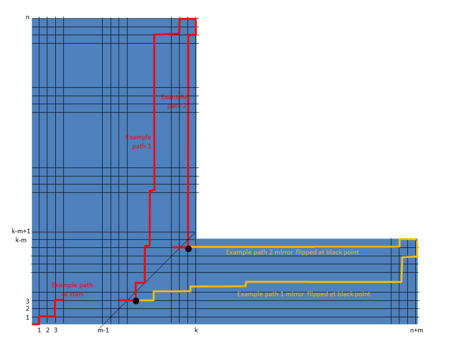
Thus the number of ways that paths can cross n - k + m - 1 = 0 is as indicated in the above formula.

See also

• Pascal's triangle

References