Young's modulus
| Young's modulus | |
|---|---|
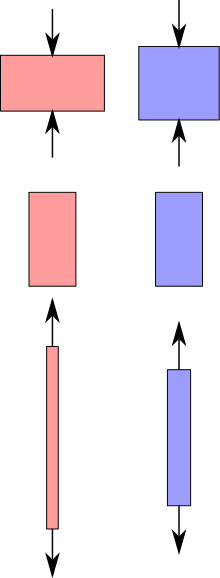 A given uniaxial stress, whether tensile (extension) or compressive (compression) creates more deformation in a material with low stiffness (red) than with a high stiffness (blue). Young's modulus is a measure of stiffness. | |
Common symbols | E, Y |
| SI unit | pascal |
| In SI base units | Pa = kg m−1 s−2 |
Derivations from other quantities | E≡σ(ε)ε=F/AΔL/L0=FL0AΔL{displaystyle Eequiv {frac {sigma (varepsilon )}{varepsilon }}={frac {F/A}{Delta L/L_{0}}}={frac {FL_{0}}{ADelta L}}} |
| Dimension | M L−1T−2 |
Young's modulus or Young modulus is a mechanical property that measures the stiffness of a solid material. It defines the relationship between stress (force per unit area) and strain (proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation.
Young's modulus is named after the 19th-century British scientist Thomas Young. However, the concept was developed in 1727 by Leonhard Euler, and the first experiments that used the concept of Young's modulus in its current form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years.[1] The term modulus is the diminutive of the Latin term modus which means measure.
Contents
1 Definition
1.1 Linear elasticity
1.2 Formula and units
2 Not to be confused with
3 Usage
3.1 Linear versus non-linear
3.2 Directional materials
4 Calculation
4.1 Force exerted by stretched or contracted material
4.2 Elastic potential energy
4.3 Relation among elastic constants
5 Approximate values
6 See also
7 References
8 Further reading
9 External links
Definition
Linear elasticity
A solid material will undergo elastic deformation when a small load is applied to it in compression or extension. Elastic deformation is reversible (the material returns to its original shape after the load is removed).
At near-zero stress and strain, the stress–strain curve is linear, and the relationship between stress and strain is described by Hooke's law that states stress is proportional to strain. The coefficient of proportionality is Young's modulus. The higher the modulus, the more stress is needed to create the same amount of strain; an idealized rigid body would have an infinite Young's modulus.
Not many materials are linear and elastic beyond a small amount of deformation.[citation needed]
Formula and units
E=σϵ{displaystyle E={frac {sigma }{epsilon }}}
E{displaystyle E}is Young's modulus, in pascal
σ{displaystyle sigma }is the uniaxial stress, or uniaxial force per unit surface, in pascal
ϵ{displaystyle epsilon }is the strain, or proportional deformation (change in length divided by original length) (nondimensional)
In practice, Young's moduli are given in megapascals (MPa or N/mm2) or gigapascals (GPa or kN/mm2).
Not to be confused with
Material stiffness should not be confused with these properties:
Strength: maximal amount of stress the material can withstand while staying in the elastic (reversible) deformation regime;- Geometric stiffness: a global characteristic of the body that depends on its shape, and not only on the local properties of the material; for instance, an I-beam has a higher bending stiffness than a rod of the same material for a given mass per length;
Hardness: relative resistance of the material's surface to penetration by a harder body;
Toughness: amount of energy that a material can absorb before fracture.
Usage
Young's modulus enables the calculation of the change in the dimension of a bar made of an isotropic elastic material under tensile or compressive loads. For instance, it predicts how much a material sample extends under tension or shortens under compression. The Young's modulus directly applies to cases of uniaxial stress, that is tensile or compressive stress in one direction and no stress in the other directions. Young's modulus is also used in order to predict the deflection that will occur in a statically determinate beam when a load is applied at a point in between the beam's supports. Other elastic calculations usually require the use of one additional elastic property, such as the shear modulus, bulk modulus or Poisson's ratio. Any two of these parameters are sufficient to fully describe elasticity in an isotropic material.
Linear versus non-linear
Young's modulus represents the factor of proportionality in Hooke's law, which relates the stress and the strain. However, Hooke's law is only valid under the assumption of an elastic and linear response. Any real material will eventually fail and break when stretched over a very large distance or with a very large force; however all solid materials exhibit nearly Hookean behavior for small enough strains or stresses. If the range over which Hooke's law is valid is large enough compared to the typical stress that one expects to apply to the material, the material is said to be linear. Otherwise (if the typical stress one would apply is outside the linear range) the material is said to be non-linear.
Steel, carbon fiber and glass among others are usually considered linear materials, while other materials such as rubber and soils are non-linear. However, this is not an absolute classification: if very small stresses or strains are applied to a non-linear material, the response will be linear, but if very high stress or strain is applied to a linear material, the linear theory will not be enough. For example, as the linear theory implies reversibility, it would be absurd to use the linear theory to describe the failure of a steel bridge under a high load; although steel is a linear material for most applications, it is not in such a case of catastrophic failure.
In solid mechanics, the slope of the stress–strain curve at any point is called the tangent modulus. It can be experimentally determined from the slope of a stress–strain curve created during tensile tests conducted on a sample of the material.
Directional materials
Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropic, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic, and Young's modulus will change depending on the direction of the force vector. Anisotropy can be seen in many composites as well. For example, carbon fiber has a much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood and reinforced concrete. Engineers can use this directional phenomenon to their advantage in creating structures.
Calculation
Young's modulus E, can be calculated by dividing the tensile stress,
σ(ε){displaystyle sigma (varepsilon )}

- E≡σ(ε)ε=F/AΔL/L0=FL0AΔL{displaystyle Eequiv {frac {sigma (varepsilon )}{varepsilon }}={frac {F/A}{Delta L/L_{0}}}={frac {FL_{0}}{ADelta L}}}
where
E is the Young's modulus (modulus of elasticity)
F is the force exerted on an object under tension;
A is the actual cross-sectional area, which equals the area of the cross-section perpendicular to the applied force;
ΔL is the amount by which the length of the object changes (ΔL is positive if the material is stretched , and negative when the material is compressed);
L0 is the original length of the object.
Force exerted by stretched or contracted material
The Young's modulus of a material can be used to calculate the force it exerts under specific strain.
- F=EAΔLL0{displaystyle F={frac {EADelta L}{L_{0}}}}
where F is the force exerted by the material when contracted or stretched by ΔL{displaystyle Delta L}
Hooke's law for a stretched wire can be derived from this formula:
- F=(EAL0)ΔL=kx{displaystyle F=left({frac {EA}{L_{0}}}right)Delta L=kx,}
where it comes in saturation
k≡EAL0{displaystyle kequiv {begin{matrix}{frac {EA}{L_{0}}}end{matrix}},}and x≡ΔL.{displaystyle xequiv Delta L.,}
But note that the elasticity of coiled springs comes from shear modulus, not Young's modulus.
Elastic potential energy
The elastic potential energy stored in a linear elastic material is given by the integral of the Hooke's law:
- Ue=∫kxdx=12kx2.{displaystyle U_{e}=int {kx},dx={frac {1}{2}}kx^{2}.}
now by expliciting the intensive variables:
- Ue=∫EAΔLL0dΔL=EAL0∫ΔLdΔL=EAΔL22L0{displaystyle U_{e}=int {frac {EADelta L}{L_{0}}},dDelta L={frac {EA}{L_{0}}}int {Delta L},dDelta L={frac {EA{Delta L}^{2}}{2L_{0}}}}
This means that the elastic potential energy density (i.e., per unit volume) is given by:
- UeAL0=EΔL22L02{displaystyle {frac {U_{e}}{AL_{0}}}={frac {E{Delta L}^{2}}{2L_{0}^{2}}}}
or, in simple notation, for a linear elastic material:
ue(ε)=∫Eεdε=12Eε2{displaystyle u_{e}(varepsilon )=int {E,varepsilon },dvarepsilon ={frac {1}{2}}E{varepsilon }^{2}}

In a nonlinear elastic material the Young's modulus is a function of the strain, so the second equivalence no longer holds and the elastic energy is not a quadratic function of the strain:
ue(ε)=∫E(ε)εdε≠12Eε2{displaystyle u_{e}(varepsilon )=int {E(varepsilon ),varepsilon },dvarepsilon neq {frac {1}{2}}E{varepsilon }^{2}}
Relation among elastic constants
For homogeneous isotropic materials simple relations exist between elastic constants (Young's modulus E, shear modulus G, bulk modulus K, and Poisson's ratio ν) that allow calculating them all as long as two are known:
- E=2G(1+ν)=3K(1−2ν).{displaystyle E=2G(1+nu )=3K(1-2nu ).,}
Approximate values

Influences of selected glass component additions on Young's modulus of a specific base glass
Young's modulus can vary somewhat due to differences in sample composition and test method. The rate of deformation has the greatest impact on the data collected, especially in polymers. The values here are approximate and only meant for relative comparison.
| Material | GPa | Mpsi |
|---|---|---|
Rubber (small strain) | 0.01–0.1[3] | 1.45–6998145000000000000♠14.5×10−3 |
Low-density polyethylene[4] | 0.11–0.86 | 1.6–6998650000000000000♠6.5×10−2 |
Diatom frustules (largely silicic acid)[5] | 0.35–2.77 | 0.05–0.4 |
PTFE (Teflon) | 0.5[3] | 0.075 |
HDPE | 0.8 | 0.116 |
Bacteriophage capsids[6] | 1–3 | 0.15–0.435 |
Polypropylene | 1.5–2[3] | 0.22–0.29 |
Polycarbonate | 2–2.4 | 0.29-0.36 |
Polyethylene terephthalate (PET) | 2–2.7[3] | 0.29–0.39 |
Nylon | 2–4 | 0.29–0.58 |
Polystyrene, solid | 3–3.5[3] | 0.44–0.51 |
Polystyrene, foam[7] | 0.0025–0.007 | 0.00036–0.00102 |
Medium-density fiberboard (MDF)[8] | 4 | 0.58 |
Wood (along grain) | 11[3] | 1.60 |
| Human Cortical Bone[9] | 14 | 2.03 |
Glass-reinforced polyester matrix[10] | 17.2 | 2.49 |
| Aromatic peptide nanotubes[11][12] | 19–27 | 2.76–3.92 |
| High-strength concrete | 30[3] | 4.35 |
| Amino-acid molecular crystals[13] | 21–44 | 3.04–6.38 |
Carbon fiber reinforced plastic (50/50 fibre/matrix, biaxial fabric) | 30–50[14] | 4.35–7.25 |
Hemp fiber[15] | 35 | 5.08 |
Magnesium metal (Mg) | 45[3] | 6.53 |
Glass (see chart)[specify] | 50–90[3] | 7.25–13.1 |
Flax fiber[16] | 58 | 8.41 |
Aluminum | 69[3] | 10 |
| Mother-of-pearl (nacre, largely calcium carbonate)[17] | 70 | 10.2 |
Aramid[18] | 70.5–112.4 | 10.2–16.3 |
Tooth enamel (largely calcium phosphate)[19] | 83 | 12 |
Stinging nettle fiber[20] | 87 | 12.6 |
Bronze | 96–120[3] | 13.9–17.4 |
Brass | 100–125[3] | 14.5–18.1 |
Titanium (Ti) | 110.3 | 16[3] |
Titanium alloys | 105–120[3] | 15–17.5 |
Copper (Cu) | 117 | 17 |
Carbon fiber reinforced plastic (70/30 fibre/matrix, unidirectional, along fibre)[21] | 181 | 26.3 |
Silicon Single crystal, different directions[22][23] | 130–185 | 18.9–26.8 |
Wrought iron | 190–210[3] | 27.6–30.5 |
Steel (ASTM-A36) | 200[3] | 29 |
| polycrystalline Yttrium iron garnet (YIG)[24] | 193 | 28 |
| single-crystal Yttrium iron garnet (YIG)[25] | 200 | 29 |
Cobalt-chrome (CoCr)[26] | 220–258 | 29 |
| Aromatic peptide nanospheres[27] | 230–275 | 33.4–40 |
Beryllium (Be)[28] | 287 | 41.6 |
Molybdenum (Mo) | 329–330[3][29][30] | 47.7–47.9 |
Tungsten (W) | 400–410[3] | 58–59 |
Silicon carbide (SiC) | 450[3] | 65 |
Tungsten carbide (WC) | 450–650[3] | 65–94 |
Osmium (Os) | 525–562[31] | 76.1–81.5 |
Single-walled carbon nanotube | 1,000+[32][33] | 150+ |
Graphene (C) | 1050[34] | 152 |
Diamond (C) | 1050–1210[35] | 152–175 |
Carbyne (C)[36] | 32100[37] | 7007321000000000000♠4,660 |
See also
- Bending stiffness
- Deflection
- Deformation
- Flexural modulus
- Hooke's law
- Impulse excitation technique
- List of materials properties
- Yield (engineering)
References
^ The Rational mechanics of Flexible or Elastic Bodies, 1638–1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "modulus of elasticity (Young's modulus), E". doi:10.1351/goldbook.M03966
^ abcdefghijklmnopqrst
"Elastic Properties and Young Modulus for some Materials". The Engineering ToolBox. Retrieved 2012-01-06..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ "Overview of materials for Low Density Polyethylene (LDPE), Molded". Matweb. Archived from the original on January 1, 2011. Retrieved February 7, 2013.
^ Subhash G, Yao S, Bellinger B, Gretz MR (2005). "Investigation of mechanical properties of diatom frustules using nanoindentation". J Nanosci Nanotechnol. 5 (1): 50–6. doi:10.1166/jnn.2005.006. PMID 15762160.
^ Ivanovska IL, de Pablo PJ, Sgalari G, MacKintosh FC, Carrascosa JL, Schmidt CF, Wuite GJ (2004). "Bacteriophage capsids: Tough nanoshells with complex elastic properties". Proc Natl Acad Sci USA. 101 (20): 7600–5. Bibcode:2004PNAS..101.7600I. doi:10.1073/pnas.0308198101. PMC 419652. PMID 15133147.
^
"Styrodur Technical Data" (PDF). BASF. Retrieved 2016-03-15.
^ "Medium Density Fiberboard (MDF) Material Properties :: MakeItFrom.com". Retrieved February 4, 2016.
^ Rho, JY (1993). "Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements". Journal of Biomechanics. 26 (2): 111–119. doi:10.1016/0021-9290(93)90042-d. PMID 8429054.
^ "Polyester Matrix Composite reinforced by glass fibers (Fiberglass)". [SubsTech] (2008-05-17). Retrieved on 2011-03-30.
^ Kol, N.; et al. (June 8, 2005). "Self-Assembled Peptide Nanotubes Are Uniquely Rigid Bioinspired Supramolecular Structures". Nano Letters. 5 (7): 1343–1346. Bibcode:2005NanoL...5.1343K. doi:10.1021/nl0505896.
^ Niu, L.; et al. (June 6, 2007). "Using the Bending Beam Model to Estimate the Elasticity of Diphenylalanine Nanotubes". Langmuir. 23 (14): 7443–7446. doi:10.1021/la7010106. PMID 17550276.
^ Azuri, I.; et al. (November 9, 2015). "Unusually Large Young's Moduli of Amino Acid Molecular Crystals". Angew. Chem. Int. Ed. 54 (46): 13566–13570. doi:10.1002/anie.201505813. PMID 26373817.
^ "Composites Design and Manufacture (BEng) – MATS 324".
^ Nabi Saheb, D.; Jog, JP. (1999). "Natural fibre polymer composites: a review". Advances in Polymer Technology. 18 (4): 351–363. doi:10.1002/(SICI)1098-2329(199924)18:4<351::AID-ADV6>3.0.CO;2-X.
^ Bodros, E. (2002). "Analysis of the flax fibres tensile behaviour and analysis of the tensile stiffness increase". Composite Part A. 33 (7): 939–948. doi:10.1016/S1359-835X(02)00040-4.
^ A. P. Jackson,J. F. V. Vincent and R. M. Turner (1988). "The Mechanical Design of Nacre". Proceedings of the Royal Society B. 234 (1277): 415–440. Bibcode:1988RSPSB.234..415J. doi:10.1098/rspb.1988.0056.
^ DuPont (2001). "Kevlar Technical Guide": 9.
^ M. Staines, W. H. Robinson and J. A. A. Hood (1981). "Spherical indentation of tooth enamel". Journal of Materials Science. 16 (9): 2551–2556. Bibcode:1981JMatS..16.2551S. doi:10.1007/bf01113595.
^ Bodros, E.; Baley, C. (15 May 2008). "Study of the tensile properties of stinging nettle fibres (Urtica dioica)". Materials Letters. 62 (14): 2143–2145. CiteSeerX 10.1.1.299.6908. doi:10.1016/j.matlet.2007.11.034.
^ Epoxy Matrix Composite reinforced by 70% carbon fibers [SubsTech]. Substech.com (2006-11-06). Retrieved on 2011-03-30.
^ "Physical properties of Silicon (Si)". Ioffe Institute Database. Retrieved on 2011-05-27.
^ E.J. Boyd; et al. (February 2012). "Measurement of the Anisotropy of Young's Modulus in Single-Crystal Silicon". Journal of Microelectromechanical Systems. 21 (1): 243–249. doi:10.1109/JMEMS.2011.2174415.
^ Chou, H. M.; Case, E. D. (November 1988). "Characterization of some mechanical properties of polycrystalline yttrium iron garnet (YIG) by non-destructive methods". Journal of Materials Science Letters. 7 (11): 1217–1220. doi:10.1007/BF00722341.
^ YIG properties
^ "Properties of cobalt-chrome alloys – Heraeus Kulzer cara". Archived from the original on 1 July 2015. Retrieved February 4, 2016.
^ Adler-Abramovich, L.; et al. (December 17, 2010). "Self-Assembled Organic Nanostructures with Metallic-Like Stiffness". Angewandte Chemie International Edition. 49 (51): 9939–9942. doi:10.1002/anie.201002037. PMID 20878815.
^ Foley, James C.; et al. (2010). "An Overview of Current Research and Industrial Practices of Be Powder Metallurgy". In Marquis, Fernand D.S. Powder Materials: Current Research and Industrial Practices III. Hoboken, NJ, USA: John Wiley & Sons, Inc. p. 263. doi:10.1002/9781118984239.ch32. ISBN 9781118984239.
^ "Molybdenum: physical properties". webelements. Retrieved January 27, 2015.
^ "Molybdenum, Mo" (PDF). Glemco. Retrieved January 27, 2014.
^ D.K.Pandey; Singh, D.; Yadawa, P. K.; et al. (2009). "Ultrasonic Study of Osmium and Ruthenium" (PDF). Platinum Metals Rev. 53 (4): 91–97. doi:10.1595/147106709X430927. Retrieved November 4, 2014.
^ L. Forro; et al. "Electronic and mechanical properties of carbon nanotubes" (PDF).
^ Y. H. Yang; Li, W. Z.; et al. (2011). "Radial elasticity of single-walled carbon nanotube measured by atomic force microscopy". Applied Physics Letters. 98 (4): 041901. Bibcode:2011ApPhL..98d1901Y. doi:10.1063/1.3546170.
^ Fang Liu; Pingbing Ming & Ju Li. "Ab initio calculation of ideal strength and phonon instability of graphene under tension" (PDF).
^ Spear and Dismukes (1994). Synthetic Diamond – Emerging CVD Science and Technology. Wiley, N.Y. p. 315. ISBN 978-0-471-53589-8.
^ Owano, Nancy (Aug 20, 2013). "Carbyne is stronger than any known material". phys.org.
^ Liu, Mingjie; Artyukhov, Vasilii I; Lee, Hoonkyung; Xu, Fangbo; Yakobson, Boris I (2013). "Carbyne From First Principles: Chain of C Atoms, a Nanorod or a Nanorope?". ACS Nano. 7 (11): 10075–10082. arXiv:1308.2258. doi:10.1021/nn404177r. PMID 24093753.
Further reading
ASTM E 111, "Standard Test Method for Young's Modulus, Tangent Modulus, and Chord Modulus"
- The ASM Handbook (various volumes) contains Young's Modulus for various materials and information on calculations. Online version (subscription required)
External links
- Matweb: free database of engineering properties for over 115,000 materials
- Young's Modulus for groups of materials, and their cost
| Conversion formulae | |||||||
|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas. | |||||||
K={displaystyle K=,}  | E={displaystyle E=,}  | λ={displaystyle lambda =,}  | G={displaystyle G=,}  | ν={displaystyle nu =,}  | M={displaystyle M=,}  | Notes | |
(K,E){displaystyle (K,,E)}  | 3K(3K−E)9K−E{displaystyle {tfrac {3K(3K-E)}{9K-E}}}  | 3KE9K−E{displaystyle {tfrac {3KE}{9K-E}}}  | 3K−E6K{displaystyle {tfrac {3K-E}{6K}}}  | 3K(3K+E)9K−E{displaystyle {tfrac {3K(3K+E)}{9K-E}}}  | |||
(K,λ){displaystyle (K,,lambda )}  | 9K(K−λ)3K−λ{displaystyle {tfrac {9K(K-lambda )}{3K-lambda }}}  | 3(K−λ)2{displaystyle {tfrac {3(K-lambda )}{2}}}  | λ3K−λ{displaystyle {tfrac {lambda }{3K-lambda }}}  | 3K−2λ{displaystyle 3K-2lambda ,}  | |||
(K,G){displaystyle (K,,G)}  | 9KG3K+G{displaystyle {tfrac {9KG}{3K+G}}}  | K−2G3{displaystyle K-{tfrac {2G}{3}}}  | 3K−2G2(3K+G){displaystyle {tfrac {3K-2G}{2(3K+G)}}}  | K+4G3{displaystyle K+{tfrac {4G}{3}}}  | |||
(K,ν){displaystyle (K,,nu )}  | 3K(1−2ν){displaystyle 3K(1-2nu ),}  | 3Kν1+ν{displaystyle {tfrac {3Knu }{1+nu }}}  | 3K(1−2ν)2(1+ν){displaystyle {tfrac {3K(1-2nu )}{2(1+nu )}}}  | 3K(1−ν)1+ν{displaystyle {tfrac {3K(1-nu )}{1+nu }}}  | |||
(K,M){displaystyle (K,,M)}  | 9K(M−K)3K+M{displaystyle {tfrac {9K(M-K)}{3K+M}}}  | 3K−M2{displaystyle {tfrac {3K-M}{2}}}  | 3(M−K)4{displaystyle {tfrac {3(M-K)}{4}}}  | 3K−M3K+M{displaystyle {tfrac {3K-M}{3K+M}}}  | |||
(E,λ){displaystyle (E,,lambda )}  | E+3λ+R6{displaystyle {tfrac {E+3lambda +R}{6}}}  | E−3λ+R4{displaystyle {tfrac {E-3lambda +R}{4}}}  | 2λE+λ+R{displaystyle {tfrac {2lambda }{E+lambda +R}}}  | E−λ+R2{displaystyle {tfrac {E-lambda +R}{2}}}  | R=E2+9λ2+2Eλ{displaystyle R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}}  | ||
(E,G){displaystyle (E,,G)}  | EG3(3G−E){displaystyle {tfrac {EG}{3(3G-E)}}}  | G(E−2G)3G−E{displaystyle {tfrac {G(E-2G)}{3G-E}}}  | E2G−1{displaystyle {tfrac {E}{2G}}-1}  | G(4G−E)3G−E{displaystyle {tfrac {G(4G-E)}{3G-E}}}  | |||
(E,ν){displaystyle (E,,nu )}  | E3(1−2ν){displaystyle {tfrac {E}{3(1-2nu )}}}  | Eν(1+ν)(1−2ν){displaystyle {tfrac {Enu }{(1+nu )(1-2nu )}}}  | E2(1+ν){displaystyle {tfrac {E}{2(1+nu )}}}  | E(1−ν)(1+ν)(1−2ν){displaystyle {tfrac {E(1-nu )}{(1+nu )(1-2nu )}}}  | |||
(E,M){displaystyle (E,,M)}  | 3M−E+S6{displaystyle {tfrac {3M-E+S}{6}}}  | M−E+S4{displaystyle {tfrac {M-E+S}{4}}}  | 3M+E−S8{displaystyle {tfrac {3M+E-S}{8}}}  | E−M+S4M{displaystyle {tfrac {E-M+S}{4M}}}  | S=±E2+9M2−10EM{displaystyle S=pm {sqrt {E^{2}+9M^{2}-10EM}}}  There are two valid solutions. The minus sign leads to ν≤0{displaystyle nu leq 0}  . . | ||
(λ,G){displaystyle (lambda ,,G)}  | λ+2G3{displaystyle lambda +{tfrac {2G}{3}}}  | G(3λ+2G)λ+G{displaystyle {tfrac {G(3lambda +2G)}{lambda +G}}}  | λ2(λ+G){displaystyle {tfrac {lambda }{2(lambda +G)}}}  | λ+2G{displaystyle lambda +2G,}  | |||
(λ,ν){displaystyle (lambda ,,nu )}  | λ(1+ν)3ν{displaystyle {tfrac {lambda (1+nu )}{3nu }}}  | λ(1+ν)(1−2ν)ν{displaystyle {tfrac {lambda (1+nu )(1-2nu )}{nu }}}  | λ(1−2ν)2ν{displaystyle {tfrac {lambda (1-2nu )}{2nu }}}  | λ(1−ν)ν{displaystyle {tfrac {lambda (1-nu )}{nu }}}  | Cannot be used when ν=0⇔λ=0{displaystyle nu =0Leftrightarrow lambda =0} | ||
(λ,M){displaystyle (lambda ,,M)}  | M+2λ3{displaystyle {tfrac {M+2lambda }{3}}}  | (M−λ)(M+2λ)M+λ{displaystyle {tfrac {(M-lambda )(M+2lambda )}{M+lambda }}}  | M−λ2{displaystyle {tfrac {M-lambda }{2}}}  | λM+λ{displaystyle {tfrac {lambda }{M+lambda }}}  | |||
(G,ν){displaystyle (G,,nu )}  | 2G(1+ν)3(1−2ν){displaystyle {tfrac {2G(1+nu )}{3(1-2nu )}}}  | 2G(1+ν){displaystyle 2G(1+nu ),}  | 2Gν1−2ν{displaystyle {tfrac {2Gnu }{1-2nu }}}  | 2G(1−ν)1−2ν{displaystyle {tfrac {2G(1-nu )}{1-2nu }}}  | |||
(G,M){displaystyle (G,,M)}  | M−4G3{displaystyle M-{tfrac {4G}{3}}}  | G(3M−4G)M−G{displaystyle {tfrac {G(3M-4G)}{M-G}}}  | M−2G{displaystyle M-2G,}  | M−2G2M−2G{displaystyle {tfrac {M-2G}{2M-2G}}}  | |||
(ν,M){displaystyle (nu ,,M)}  | M(1+ν)3(1−ν){displaystyle {tfrac {M(1+nu )}{3(1-nu )}}}  | M(1+ν)(1−2ν)1−ν{displaystyle {tfrac {M(1+nu )(1-2nu )}{1-nu }}}  | Mν1−ν{displaystyle {tfrac {Mnu }{1-nu }}}  | M(1−2ν)2(1−ν){displaystyle {tfrac {M(1-2nu )}{2(1-nu )}}}  | |||













