Orthorhombic crystal system
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
Contents
1 Bravais lattices
1.1 Two-dimensional
1.2 Three-dimensional
2 Crystal classes
3 See also
4 References
5 Further reading
Bravais lattices
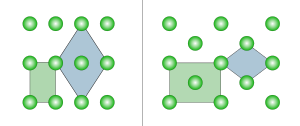
Rectangular vs rhombic unit cells for the 2D orthorhombic lattices. The swapping of centering type when the unit cell is changed also applies for the 3D orthorhombic lattices
Two-dimensional
In two dimensions there are two orthorhombic Bravais lattices: Primitive rectangular and centered rectangular. The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell.
Three-dimensional
In three dimensions, there are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.
| Bravais lattice | Primitive orthorhombic | Base-centered orthorhombic | Body-centered orthorhombic | Face-centered orthorhombic |
|---|---|---|---|---|
Pearson symbol | oP | oS | oI | oF |
| Standard unit cell | 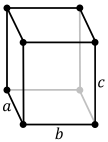 |  |  |  |
| Right rhombic prism unit cell |  |  |  |  |
In the orthorhombic system there is a rarely used second choice of crystal axes that results in a unit cell with the shape of a right rhombic prism;[1] it can be constructed because the rectangular two-dimensional base layer can also be described with rhombic axes. In this axis setting, the primitive and base-centered lattices swap in centering type, while the same thing happens with the body-centered and face-centered lattices.
Crystal classes
The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,[2]orbifold notation, type, and space groups are listed in the table below.
| # | Point group | Type | Example | Space groups | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Base-centered | Face-centered | Body-centered | |||
| 16-24 | Rhombic disphenoidal | D2 (V) | 222 | 222 | [2,2]+ | enantiomorphic | epsomite | P222, P2221, P21212, P212121 | C2221, C222 | F222 | I222, I212121 |
| 25-46 | Rhombic pyramidal | C2v | mm2 | *22 | [2] | polar | hemimorphite, bertrandite | Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2 | Cmm2, Cmc21, Ccc2 Amm2, Aem2, Ama2, Aea2 | Fmm2, Fdd2 | Imm2, Iba2, Ima2 |
| 47-74 | Rhombic dipyramidal | D2h (Vh) | mmm | *222 | [2,2] | centrosymmetric | olivine, aragonite, marcasite | Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma | Cmcm, Cmca, Cmmm, Cccm, Cmme, Ccce | Fmmm, Fddd | Immm, Ibam, Ibca, Imma |
See also
- Crystal structure
- Overview of all space groups
References
^ See Hahn (2002), p. 746, row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90°
^ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ "The 32 crystal classes". Retrieved 2018-06-19.
Further reading
Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.