Wsrtjtyk

Earth's atmospheric transmittance over 1 nautical mile sea level path (infrared region^[1]). Because of the natural radiation of the hot atmosphere, the intensity of radiation is different from the transmitted part.

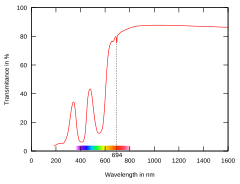
Transmittance of ruby in optical and near-IR spectra. Note the two broad blue and green absorption bands and one narrow absorption band on the wavelength of 694 nm, which is the wavelength of the ruby laser.

Transmittance of the surface of a material is its effectiveness in transmitting radiant energy. It is the fraction of incident electromagnetic power that is transmitted through a sample, in contrast to the transmission coefficient, which is the ratio of the transmitted to incident electric field.^[2]

Internal transmittance refers to energy loss by absorption, whereas (total) transmittance is that due to absorption, scattering, reflection, etc.

Mathematical definitions

Hemispherical transmittance

Hemispherical transmittance of a surface, denoted T, is defined as^[3]

T=ΦetΦei,{displaystyle T={frac {Phi _{mathrm {e} }^{mathrm {t} }}{Phi _{mathrm {e} }^{mathrm {i} }}},}

where

• Φ_e^t is the radiant flux transmitted by that surface;


• Φ_eⁱ is the radiant flux received by that surface.

Spectral hemispherical transmittance

Spectral hemispherical transmittance in frequency and spectral hemispherical transmittance in wavelength of a surface, denoted T_ν and T_λ respectively, are defined as^[3]

Tν=Φe,νtΦe,νi,{displaystyle T_{nu }={frac {Phi _{mathrm {e} ,nu }^{mathrm {t} }}{Phi _{mathrm {e} ,nu }^{mathrm {i} }}},}

Tλ=Φe,λtΦe,λi,{displaystyle T_{lambda }={frac {Phi _{mathrm {e} ,lambda }^{mathrm {t} }}{Phi _{mathrm {e} ,lambda }^{mathrm {i} }}},}

where

• Φ_e,ν^t is the spectral radiant flux in frequency transmitted by that surface;


• Φ_e,νⁱ is the spectral radiant flux in frequency received by that surface;


• Φ_e,λ^t is the spectral radiant flux in wavelength transmitted by that surface;


• Φ_e,λⁱ is the spectral radiant flux in wavelength received by that surface.

Directional transmittance

Directional transmittance of a surface, denoted T_Ω, is defined as^[3]

TΩ=Le,ΩtLe,Ωi,{displaystyle T_{Omega }={frac {L_{mathrm {e} ,Omega }^{mathrm {t} }}{L_{mathrm {e} ,Omega }^{mathrm {i} }}},}

where

• 
  L_e,Ω^t is the radiance transmitted by that surface;


• 
  L_e,Ωⁱ is the radiance received by that surface.

Spectral directional transmittance

Spectral directional transmittance in frequency and spectral directional transmittance in wavelength of a surface, denoted T_ν,Ω and T_λ,Ω respectively, are defined as^[3]

Tν,Ω=Le,Ω,νtLe,Ω,νi,{displaystyle T_{nu ,Omega }={frac {L_{mathrm {e} ,Omega ,nu }^{mathrm {t} }}{L_{mathrm {e} ,Omega ,nu }^{mathrm {i} }}},}

Tλ,Ω=Le,Ω,λtLe,Ω,λi,{displaystyle T_{lambda ,Omega }={frac {L_{mathrm {e} ,Omega ,lambda }^{mathrm {t} }}{L_{mathrm {e} ,Omega ,lambda }^{mathrm {i} }}},}

where

• 
  L_e,Ω,ν^t is the spectral radiance in frequency transmitted by that surface;


• 
  L_e,Ω,νⁱ is the spectral radiance received by that surface;


• 
  L_e,Ω,λ^t is the spectral radiance in wavelength transmitted by that surface;


• 
  L_e,Ω,λⁱ is the spectral radiance in wavelength received by that surface.

Beer–Lambert law

By definition, transmittance is related to optical depth and to absorbance as

T=e−τ=10−A,{displaystyle T=e^{-tau }=10^{-A},}

where

• 
  τ is the optical depth;


• 
  A is the absorbance.

The Beer–Lambert law states that, for N attenuating species in the material sample,

T=e−∑i=1Nσi∫0ℓni(z)dz=10−∑i=1Nεi∫0ℓci(z)dz,{displaystyle T=e^{-sum _{i=1}^{N}sigma _{i}int _{0}^{ell }n_{i}(z)mathrm {d} z}=10^{-sum _{i=1}^{N}varepsilon _{i}int _{0}^{ell }c_{i}(z)mathrm {d} z},}

or equivalently that

τ=∑i=1Nτi=∑i=1Nσi∫0ℓni(z)dz,{displaystyle tau =sum _{i=1}^{N}tau _{i}=sum _{i=1}^{N}sigma _{i}int _{0}^{ell }n_{i}(z),mathrm {d} z,}

A=∑i=1NAi=∑i=1Nεi∫0ℓci(z)dz,{displaystyle A=sum _{i=1}^{N}A_{i}=sum _{i=1}^{N}varepsilon _{i}int _{0}^{ell }c_{i}(z),mathrm {d} z,}

where

• 
  σ_i is the attenuation cross section of the attenuating specie i in the material sample;


• 
  n_i is the number density of the attenuating specie i in the material sample;


• 
  ε_i is the molar attenuation coefficient of the attenuating specie i in the material sample;


• 
  c_i is the amount concentration of the attenuating specie i in the material sample;


• 
  ℓ is the path length of the beam of light through the material sample.

Attenuation cross section and molar attenuation coefficient are related by

εi=NAln⁡10σi,{displaystyle varepsilon _{i}={frac {mathrm {N_{A}} }{ln {10}}},sigma _{i},}

and number density and amount concentration by

ci=niNA,{displaystyle c_{i}={frac {n_{i}}{mathrm {N_{A}} }},}

where N_A is the Avogadro constant.

In case of uniform attenuation, these relations become^[4]

T=e−∑i=1Nσiniℓ=10−∑i=1Nεiciℓ,{displaystyle T=e^{-sum _{i=1}^{N}sigma _{i}n_{i}ell }=10^{-sum _{i=1}^{N}varepsilon _{i}c_{i}ell },}

or equivalently

τ=∑i=1Nσiniℓ,{displaystyle tau =sum _{i=1}^{N}sigma _{i}n_{i}ell ,}

A=∑i=1Nεiciℓ.{displaystyle A=sum _{i=1}^{N}varepsilon _{i}c_{i}ell .}

Cases of non-uniform attenuation occur in atmospheric science applications and radiation shielding theory for instance.

SI radiometry units

See also

• Opacity (optics)

References